Developing for Windows Phone and Xbox Live : Projection Matrix

Perspective

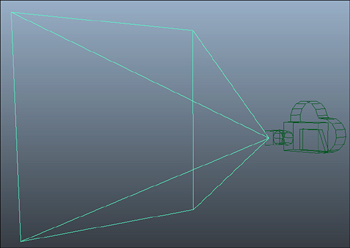
The perspective matrix lets you define the viewing frustum. To visualize what this is, imagine a pyramid. The tip of the pyramid is the location of the camera (or your eye). Anything that exists inside that pyramid can be seen; anything that exists outside of the pyramid cannot be seen. The various methods to create perspective projection matrices are used to define the size and shape of this pyramid. See Figure 1.

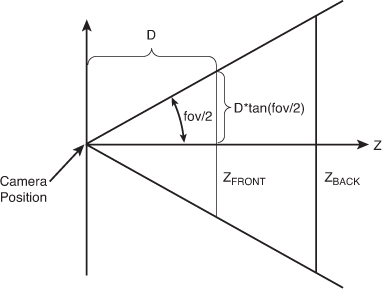
First, let’s look at the matrix used in the example. It was created using the CreatePerspectiveFieldOfView method, which has a few parameters. The first is the field of view parameter, the second is the aspect ratio, and the last two are the near and far planes, but what do these actually mean? The field of view is the angle that the top of the pyramid forms and is specified in radians. In the example, we used an angle of 45 degrees, which is somewhat common. If you used 90 degrees (MathHelper.PiOver2) instead, you’d have a much larger field of view, and thus, a larger viewing area. This would cause your rendered objects to appear smaller because the same screen area would have to render a larger world area (see Figure 2 for more information on the math of the field of view or fov).

The second parameter is the aspect ratio, which is simply the width of your scene divided by the height of your scene. Notice here that you use the Viewport property of the GraphicsDevice and you use the AspectRatio property from that. This is the most common aspect ratio you use, but if you render to something other than the back buffer (say a render target), you might want to render at a different aspect ratio. The aspect ratio here is just like the aspect ratio you see on televisions. Standard-definition televisions have a 1.33 (4/3) aspect ratio, whereas most high-definition televisions have a 1.77 (16/9) aspect ratio. Most of the old resolutions you’ve seen in computers were 1.33 (4/3) aspect ratios (640×480, 800×600, 1024×768, and so on).

The last two parameters are the near and the far planes of the frustum. Anything closer than the near plane or anything farther than the far plane is not visible. You can think of the far plane as the base of the pyramid, whereas the near plane is where you would “cut off” the top of the pyramid.

See Figure 2 for more information on the math for a field of view projection matrix.

Using the field of view is one way to create a perspective projection matrix, but not the only way. There are two other helper methods you can use, namely CreatePerspective and CreatePerspectiveOffCenter. Each of these creates your pyramid in slightly different ways, but before we get to that, let’s modify the example to draw a lot of boxes so it’s easier to see how the changes behave. Replace your draw code with the following (this might seem way more complicated than it is) to see a series of boxes like you see in Figure 3:

protected override void Draw(GameTime gameTime)
{
    const int numberBoxes = 3;
    const int radiusMultiple = numberBoxes + 1;
    GraphicsDevice.Clear(Color.CornflowerBlue);
    float radius = model.Meshes[0].BoundingSphere.Radius;
Matrix view = Matrix.CreateLookAt(
        new Vector3(0, radius * radiusMultiple,
            radius * (radiusMultiple * radiusMultiple)),
       new Vector3((numberBoxes / 2) * (radius * radiusMultiple) - 1,
            (numberBoxes / 2) * (radius * radiusMultiple) - 1, 0),
            Vector3.Up);
Matrix proj = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4,
        GraphicsDevice.Viewport.AspectRatio, 1.0f, 100.0f);
    for (int x = 0; x < numberBoxes; x++)
    {
        for (int y = 0; y < numberBoxes; y++)
        {
            Vector3 pos = new Vector3((y * (radius * radiusMultiple)) - 1,
                (x * (radius * radiusMultiple)) - 1, -(y + x));
            model.Draw(Matrix.CreateTranslation(pos), view, proj);
        }
    }
    base.Draw(gameTime);
}

					  

Figure 3. The view of a bunch of boxes

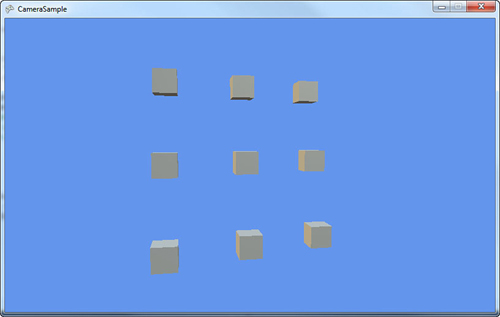
Although this seems more complicated than it is, all you’re doing here is drawing nine different boxes. They’re rendered in a square pattern with each one rendered at a different spot in the world and at a variety of different depths. You should notice how ones that are farther away are slightly smaller.

The CreatePerspective method takes only four parameters to describe what your pyramid should look like. The first one is the width of the top of the pyramid (where the near plane cuts it off), and the second is the height of the same. The third parameter is the distance to the near plane, and the fourth is the distance to the far plane (or the base of the pyramid). Modify your matrix creation as follows:

Matrix proj = Matrix.CreatePerspective(1.0f, 0.5f, 1.0f, 100.0f);

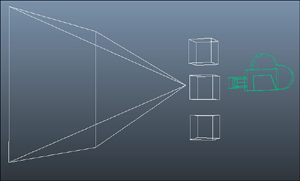
If you run the program now, notice that the picture has changed somewhat dramatically. All nine boxes don’t even appear fully onscreen anymore! This is because you changed the shape of your viewing frustum (or the pyramid), and portions of those boxes are now outside of it. See Figure 4.

The CreatePerspective method assumes that you are looking at the center point of the near plane (formed by the width and height), but that isn’t a requirement either. You can use the CreatePerspectiveOffCenter method, which is similar to the nonoff center method. Rather than a width and height being passed in, you instead must pass in the left, right, top, and bottom positions. For example, if you use the following instead of the CreatePerspective method you used earlier, you would get the same output:

proj = Matrix.CreatePerspectiveOffCenter(-0.5f, 0.5f, -0.25f, 0.25f, 1.0f, 100.0f);

					  

This is because you have the same width and height, and they are centered. Using this method enables you even more control over the location and size of the viewing frustum.

There is also another common type of projection matrix, the orthographic projection.

Orthographic

Much like a perspective matrix, an orthographic matrix builds a viewing frustum, but instead of a pyramid shaped structure, it is more rectangular. The viewing frustum does not get larger between the near plane and the far plane, and no perspective foreshortening occurs. All objects of the same size are rendered the same size, regardless of how far they are from the camera.

There are two helper methods to create these types of projection matrix: CreateOrthographic and CreateOrthographicOffCenter. Much like the perspective counterparts, these describe the orthographic volume, with the former being centered and the latter capable of being off center. If you replaced your project matrix with the following, you would see all nine boxes, but they’d all appear on the same plane:

proj = Matrix.CreateOrthographic(15.0f, 15.5f, 1.0f, 100.0f);

With the basics of projection matrices and view matrices out of the way, now you can actually create some camera types!